프로그래머스: [1차] 추석 트래픽⭐⭐⭐
카테고리: Programmers
태그: Algorithm, Blog, C++, Programmers
난이도 ⭐⭐⭐
유형 : 구현
🧐 문제
문제 설명
이번 추석에도 시스템 장애가 없는 명절을 보내고 싶은 어피치는 서버를 증설해야 할지 고민이다. 장애 대비용 서버 증설 여부를 결정하기 위해 작년 추석 기간인 9월 15일 로그 데이터를 분석한 후 초당 최대 처리량을 계산해보기로 했다. 초당 최대 처리량은 요청의 응답 완료 여부에 관계없이 임의 시간부터 1초(=1,000밀리초)간 처리하는 요청의 최대 개수를 의미한다.
입력 형식
solution함수에 전달되는lines배열은 N(1 ≦ N ≦ 2,000)개의 로그 문자열로 되어 있으며, 각 로그 문자열마다 요청에 대한 응답완료시간 S와 처리시간 T가 공백으로 구분되어 있다.- 응답완료시간 S는 작년 추석인 2016년 9월 15일만 포함하여 고정 길이
2016-09-15 hh:mm:ss.sss형식으로 되어 있다. - 처리시간 T는
0.1s,0.312s,2s와 같이 최대 소수점 셋째 자리까지 기록하며 뒤에는 초 단위를 의미하는s로 끝난다. - 예를 들어, 로그 문자열
2016-09-15 03:10:33.020 0.011s은 “2016년 9월 15일 오전 3시 10분 33.010초“부터 “2016년 9월 15일 오전 3시 10분 33.020초“까지 “0.011초” 동안 처리된 요청을 의미한다. (처리시간은 시작시간과 끝시간을 포함) - 서버에는 타임아웃이 3초로 적용되어 있기 때문에 처리시간은 0.001 ≦ T ≦ 3.000이다.
lines배열은 응답완료시간 S를 기준으로 오름차순 정렬되어 있다.
출력 형식
solution함수에서는 로그 데이터lines배열에 대해 초당 최대 처리량을 리턴한다.
입출력 예제
예제1
-
입력: [
“2016-09-15 01:00:04.001 2.0s”,
“2016-09-15 01:00:07.000 2s”
]
-
출력: 1
예제2
-
입력: [
“2016-09-15 01:00:04.002 2.0s”,
“2016-09-15 01:00:07.000 2s”
]
- 출력: 2
-
설명: 처리시간은 시작시간과 끝시간을 포함하므로
첫 번째 로그는
01:00:02.003 ~ 01:00:04.002에서 2초 동안 처리되었으며,두 번째 로그는
01:00:05.001 ~ 01:00:07.000에서 2초 동안 처리된다.따라서, 첫 번째 로그가 끝나는 시점과 두 번째 로그가 시작하는 시점의 구간인
01:00:04.002 ~ 01:00:05.0011초 동안 최대 2개가 된다.
예제3
-
입력: [
“2016-09-15 20:59:57.421 0.351s”,
“2016-09-15 20:59:58.233 1.181s”,
“2016-09-15 20:59:58.299 0.8s”,
“2016-09-15 20:59:58.688 1.041s”,
“2016-09-15 20:59:59.591 1.412s”,
“2016-09-15 21:00:00.464 1.466s”,
“2016-09-15 21:00:00.741 1.581s”,
“2016-09-15 21:00:00.748 2.31s”,
“2016-09-15 21:00:00.966 0.381s”,
“2016-09-15 21:00:02.066 2.62s”
]
- 출력: 7
-
설명: 아래 타임라인 그림에서 빨간색으로 표시된 1초 각 구간의 처리량을 구해보면
(1)은 4개,(2)는 7개,(3)는 2개임을 알 수 있다. 따라서 초당 최대 처리량은 7이 되며, 동일한 최대 처리량을 갖는 1초 구간은 여러 개 존재할 수 있으므로 이 문제에서는 구간이 아닌 개수만 출력한다.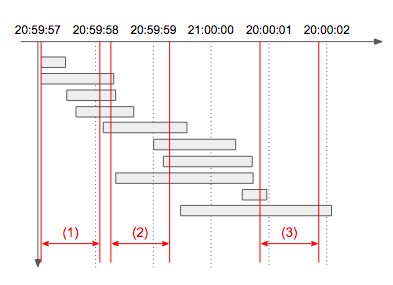
✏️ 나의 풀이
#include <bits/stdc++.h>
using namespace std;
bool comp(pair<bool,int> a, pair<bool,int> b) {
return a.second < b.second;
}
// 시간을 ms 단위로 변경 후, 시작/종료 시간 반환
pair<pair<bool,int>,pair<bool,int>> log2times(string& line) {
int hh = stoi(line.substr(11,2));
int mm = stoi(line.substr(14,2));
int ss_ms = (int)(round(stof(line.substr(17,6))*1000));
int endTime = hh*3600*1000 + mm*60*1000 + ss_ms;
string t = line.substr(24,line.size()-25);
int processMs = (int)(stof(t)*1000);
int startTime = endTime - processMs + 1;
return {
{false, startTime},
{true, endTime}
};
}
int solution(vector<string> lines) {
// 시작/종료 시간을 포함하는 벡터
vector<pair<bool,int>> timeline;
for(int i=0; i<lines.size(); i++) {
pair<pair<bool,int>,pair<bool,int>> times = log2times(lines[i]);
timeline.push_back(times.first);
timeline.push_back(times.second);
}
// 타임라인을 시간 기준으로 오름차순 정렬
sort(timeline.begin(), timeline.end(), comp);
// cnt: 현재 처리중인 개수
// max_cnt: 1초간 처리 최대 개수
int cnt = 0;
int max_cnt = 0;
for(int i=0; i<timeline.size(); i++) {
// 시작시간인 경우, cnt++;
if(timeline[i].first == 0) { cnt++; }
// 완료시간인 경우, 계산 후 cnt--;
else if(timeline[i].first == 1) {
int temp_cnt = cnt;
int border_start = timeline[i].second;
int border_end = border_start + 999;
for(int j=i; j<timeline.size(); j++) {
if(timeline[j].second > border_end) break;
if(timeline[j].first == 0) temp_cnt++;
}
max_cnt = max(temp_cnt, max_cnt);
cnt--;
}
}
return max_cnt;
}
각 로그는 아래와 같은 정보를 가지고 있다.
- 끝난 시각 (hh:mm:ss.sss)
- 처리 시간 (T초)
이를 통해 각 로그의 시작 시간과 종료 시간을 알 수 있다.
로그를 기반으로 시작 시간과 종료 시간을 ms로 변환한 후, 하나의 리스트에 담아 시간 기준으로 정렬하였다.
- 타임라인 순회
- 시작 시간 이벤트면, 현재 처리 요청 개수 cnt++;
- 종료 시간 이벤트면:
- 종료 시점을 기준으로 1초 동안 (즉,
[endTime, endTime + 999]) 얼마나 많은 요청이 처리중인지 센다. - 이때
cnt는 이미 처리 중이던 요청 수이므로, 새로 시작되는 요청 수를 더해temp_cnt계산 max_cnt를 업데이트- 그리고 이벤트가 종료되었으므로
cnt—
- 성능 : 최악의 경우 $O(N^2)$이 될 수 있다.
✔️ 다른 사람의 풀이
#include <string>
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;
#define BUFF_SIZE 86400000
int buff[BUFF_SIZE] = {0};
int solution(vector<string> lines) {
int answer = 0;
for (int i = 0; i < lines.size(); i++)
{
int end=0;
int elapsed_time;
int y, m, d, hh, mm, ss, zzz;
double elapsed_double;
sscanf(lines[i].c_str(), "%d-%d-%d %d:%d:%d.%d %lfs", &y, &m, &d, &hh, &mm,&ss, &zzz, &elapsed_double);
elapsed_time = (int)(elapsed_double * 1000);
end += hh*60;
end += mm;
end *= 60;
end += ss;
end *= 1000;
end += zzz;
for (int j = end - (elapsed_time-1) -999; j <= end; j++)
{
if (j < 0 || j >= BUFF_SIZE)
continue;
buff[j] += 1;
answer = max(answer, buff[j]);
}
}
return answer;
}
나의 코드와는 달리 sscanf를 사용하여 처리하고 있다.
substr와 stoi, stof를 통해 변환하는 것과 달리 매우 깔끔한 코드를 보여준다.
- 아이디어
- 로그를 한 줄씩 읽고, 끝난 시각과 처리 시간을 구한다.
- 시작 시점을 기점으로 1초전부터, 끝난 시점까지가 순회 범위
- 해당 로그가 영향을 미치는 모든 구간을 순회하며, 그 구간의 buff에 +1
- answer(즉, 1초간 최대 처리 개수)를 업데이트한다.
- 성능 : 최악의 경우 \(O(N^2)\)이 될 수 있다.
🧐 성능 비교
| 테스트 케이스 / 풀이 | 나의 풀이 | 다른 사람의 풀이 |
|---|---|---|
| 테스트 1 〉 | 통과 (0.02ms, 4.22MB) | 통과 (0.09ms, 4.13MB) |
| 테스트 2 〉 | 통과 (0.51ms, 4.14MB) | 통과 (5.97ms, 6.18MB) |
| 테스트 3 〉 | 통과 (0.66ms, 4.22MB) | 통과 (4.19ms, 4.15MB) |
| 테스트 4 〉 | 통과 (0.02ms, 4.21MB) | 통과 (0.04ms, 4.15MB) |
| 테스트 5 〉 | 통과 (0.07ms, 4.21MB) | 통과 (0.52ms, 4.22MB) |
| 테스트 6 〉 | 통과 (0.07ms, 4.18MB) | 통과 (0.25ms, 4.14MB) |
| 테스트 7 〉 | 통과 (0.56ms, 4.22MB) | 통과 (10.22ms, 13.6MB) |
| 테스트 8 〉 | 통과 (0.51ms, 4.14MB) | 통과 (8.45ms, 11.8MB) |
| 테스트 9 〉 | 통과 (0.07ms, 4.21MB) | 통과 (0.88ms, 4.58MB) |
| 테스트 10 〉 | 통과 (0.02ms, 4.28MB) | 통과 (0.07ms, 4.17MB) |
| 테스트 11 〉 | 통과 (0.02ms, 4.14MB) | 통과 (0.10ms, 4.14MB) |
| 테스트 12 〉 | 통과 (0.45ms, 4.15MB) | 통과 (12.64ms, 15.3MB) |
| 테스트 13 〉 | 통과 (0.11ms, 4.14MB) | 통과 (0.60ms, 3.92MB) |
| 테스트 14 〉 | 통과 (0.02ms, 4.15MB) | 통과 (0.02ms, 4.23MB) |
| 테스트 15 〉 | 통과 (0.02ms, 4.21MB) | 통과 (0.05ms, 4.24MB) |
| 테스트 16 〉 | 통과 (0.04ms, 4.14MB) | 통과 (0.05ms, 3.96MB) |
| 테스트 17 〉 | 통과 (0.02ms, 4.14MB) | 통과 (0.03ms, 4.14MB) |
| 테스트 18 〉 | 통과 (2.45ms, 4.32MB) | 통과 (8.65ms, 4.21MB) |
| 테스트 19 〉 | 통과 (0.91ms, 4.22MB) | 통과 (32.53ms, 31.6MB) |
| 테스트 20 〉 | 통과 (0.93ms, 4.27MB) | 통과 (19.10ms, 16.2MB) |
| 테스트 21 〉 | 통과 (0.02ms, 3.88MB) | 통과 (0.02ms, 3.8MB) |
| 테스트 22 〉 | 통과 (0.02ms, 3.73MB) | 통과 (0.03ms, 4.22MB) |
최악의 경우 \(O(N^2)\)인 점은 같다.
하지만 처리 시간의 최대 값은 3000ms 이므로, 나의 코드가 더 최적화가 좋은 것을 확인할 수 있다.
실제로 테스트 케이스 결과에서도 유의미한 차이를 보였다.
댓글남기기